
4. JULIA SETS WITH MATLAB



Since it is always possible to represent a COMPLEX variable as a couple of real variables in Gauss' plane, MATLAB proves extremely efficient in calculating and painting the approximate domains of non convergence of the series of complex functions needed in the study of JULIA sets.
A variant of the classical escape method is applied here: instead of evaluating the number of cycles required in order that the modulus of the partial sum exceeds a fixed bound, we evaluate the value of that modulus for a fixed number of cycles.
That procedure:

COLORMAPS
The use of the different system MATLAB colormaps provides different effects; in particular colormap copper produces interesting metal coloured shapes, while less uniform maps like jet and prism reveal the internal structure of the Julia set.
Here are some examples all with f(z)=z2+c.

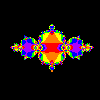 c=-.745429 MATLAB Script J.1
c=-.745429 MATLAB Script J.1

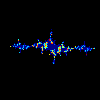 c=-1.3+0.1*i MATLAB Script J.2
c=-1.3+0.1*i MATLAB Script J.2

 c= 0.27334-0.00742*i MATLAB Script J.3
c= 0.27334-0.00742*i MATLAB Script J.3

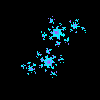 c= 0.11031031-0.67037*i MATLAB Script J.4
c= 0.11031031-0.67037*i MATLAB Script J.4

 c=-0.488679-0.56790*i MATLAB Script J.5
c=-0.488679-0.56790*i MATLAB Script J.5

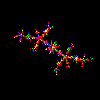 c=-0.561321+0.641000*i MATLAB Script J.6
c=-0.561321+0.641000*i MATLAB Script J.6

 c=-0.561321+0.641000*i , colormap cool
c=-0.561321+0.641000*i , colormap cool

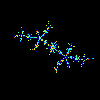 c=-0.561321+0.641000*i, colormap jet
c=-0.561321+0.641000*i, colormap jet

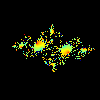 c=-.745429+.11308*i MATLAB Script J.7
c=-.745429+.11308*i MATLAB Script J.7

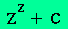 sets with MATLAB
sets with MATLAB

