The following pages represent a new section of my Fractal Gallery.

Here I want to present an alternative graphical way to navigate across Mandelbrot and Julia sets, based on the technique of CLICKING virtual maps.

Together with each map and image you will find some explanation related to the parameters and computer programs.

Choose the map you are interested in! Or, if you like, see all of them...

To navigate into the Mandelbrot set click the Mandelbrot zoom map

To navigate into into the Seahorse Julia set click the Julia zoom map

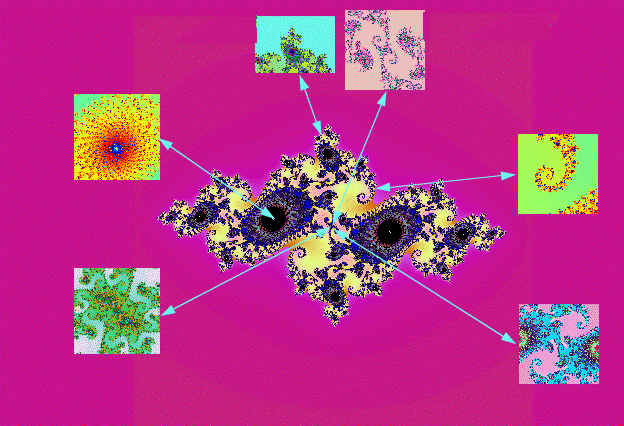
For a tour of Julia sets along the boundary of Mandelbrot set

click the Map of Julia sets on Mandelbrot boundary

---

MANDELBROT ZOOM MAP

Click on one of the small images into the Map to see the magnification of the Mandelbrot set in full size. You will notice that the colour palette has been chosen differently for each image to reach the best chromatic effect.

JULIA ZOOM MAP

In this map I propose some magnified images of the Seahorse Julia set, the most spectacular of the Julia sets, which is obtained when the complex constant parameter c = 0.74543 + i 0.11301.

MAP OF JULIA SETS ON MANDELBROT BOUNDARY

The Mandelbrot set is a sort of book each page of which is a picture of a Julia set, corresponding to a value of the parameter c identifying a point of the Mandelbrot set.

In a more mathematical language we say that each Julia set may be represented by a point in a complex parameter space: each point of this space lies inside the Mandelbrot set if the Julia set is connected, while it lies outside the Mandelbrot set when the corresponding Julia set is not connected (Fatou dust). When the point labelled by the parameter c runs along the fractal boundary of the Mandelbrot set, the Julia set modifies its shape in a very elegant way.

The map I present here shows some of the shapes of the Julia sets corresponding to values of c moving in a neighbourhood of the boundary of the Mandelbrot set.

BACK TO CIRAM HOME PAGE