Fractal Gallery is small exhibition of color fractal images of various kinds which has been built starting from different mathematical problems and techniques, as an example of the ways a computer machine can be forced to generate very elegant shapes which are also of special interest for mathematicians. In the following you will find images of:
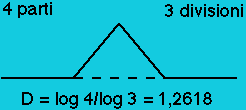
![]() Fractals generated by the iteration of a geometric procedure like the
curve of Von Koch;
Fractals generated by the iteration of a geometric procedure like the
curve of Von Koch;
![]() Fractals generated by iteration of complex functions like the Mandelbrot set and Julia sets;
Fractals generated by iteration of complex functions like the Mandelbrot set and Julia sets;
![]() Fractals reproducing realistic shapes like trees, ferns, mountains and so on.
Fractals reproducing realistic shapes like trees, ferns, mountains and so on.
Together with the images you can find some information about the mathematical problems and computer programs which can generate such plots.
Enjoy a nice tour to Fractal Gallery!

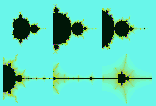
Nesting the same procedure you can generate higher order approximations of the curve of Von Kock which is the fractal limiting curve. Here you see the second, third and forth order approximations resembling snow christals. If you are interested to the corresponding PostScript programs click on the row at the right each figure.
![]()
![]()
![]() You must click on each image if you want to see it in full size.
You must click on each image if you want to see it in full size.
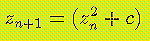

An alternative and generally better way to build up color images of the Mandelbrot set consists in writing down a prgram, in some suitable language (like MandelbrotX2.bas in Quick Basic for MacIntosh), which creates a sequential text file containing the escape speeds, i.e. the number of terms needed for the partial sum of the series to become greater than the fixed upperbound. The text file can be read by a program, like e.g. NCSA DataScope for MacIntosh (a Unix version is also available), which converts each number into a colour density plot according to a chosen color palette. One of the advantage of such a procedure is related to the capability of changing the choice of the color palette in order to reach the best chromatic effect. The files can be saved in the significantly shorter format HDF. A collection of images is presented here.
![]()
![]()
![]() Click that image to see it in full size.
Click that image to see it in full size.
 A zoom in Mandelbrot set shows another Mandelbrot
A zoom in Mandelbrot set shows another Mandelbrot
 Mandelbrot set is selfsimilar along its symmetry axis
Mandelbrot set is selfsimilar along its symmetry axis
 A deeper zoom requires double precision calculations
A deeper zoom requires double precision calculations
![]()
![]()
![]() Click that image to see it in full size.
Click that image to see it in full size.
To each fixed value of the parameter c of the recursion law which defines the sequence we introduced to define the Mandelbrot set we may associate a convergence domain of the same series respect to the value complex variable z for n = 0, when it is not fixed to null value but it runs all over the complex plane. Such domain is the Julia set corresponding to that value of c. A simple variant of the program MadelbrotX1.bas is represented by the program JuliaX1.bas which can generate the following 8 colour image.

The program JuliaX2.bas generates text files which can be read by NCSA DataScope and saved in HDF format. Here are some plots.
 Julia sets when c is moving along the boundery of Mandelbrot
set
Julia sets when c is moving along the boundery of Mandelbrot
set
 Julia sets when c is moving along an axis of Mandelbrot
set crossing the Seahorse valley
Julia sets when c is moving along an axis of Mandelbrot
set crossing the Seahorse valley
 A zoom into the seahorse Julia set
A zoom into the seahorse Julia set
![]()
![]()
![]() Click on each image to see it in full size.
Click on each image to see it in full size.
Three dimensional plots of Mandelbrot and Julia sets are presented here in which the quote is proportional to the escape speed of convergence of the truncated series.
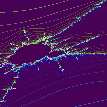 A night view of the Mandelbrot set
A night view of the Mandelbrot set
 A 3D view of Mandelbrot seahorses
A 3D view of Mandelbrot seahorses
 The Mandelbrot set like a gothic cathedral
The Mandelbrot set like a gothic cathedral
 Mandelbrot set like an iced lake
Mandelbrot set like an iced lake
Fractals reproducing a realistic shape can be generated in several ways. The simplest way is that of iterating an assigned function many many times and to plot the result at each iteration; the choice of the colour may be random or other. A more refined procedure is obtained by the iteration of one or more affine transformations of the type
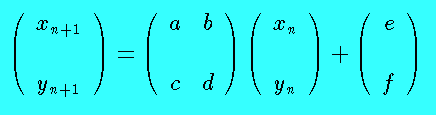
![]() Fractals generated by iterated functions
Fractals generated by iterated functions
 Program InsectX1.bas A small insect
Program InsectX1.bas A small insect
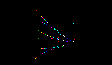
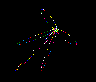 Program InsectX2.bas Another example
of small insect
Program InsectX2.bas Another example
of small insect
 Program WebX.bas A shape resembling a web
Program WebX.bas A shape resembling a web
 Program FlowersX.bas Fractal flowers
Program FlowersX.bas Fractal flowers
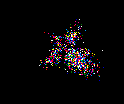 Program GalaxyX.bas A galaxy
Program GalaxyX.bas A galaxy
![]()
![]()
![]() You must click on each image if you want to see it in full size.
You must click on each image if you want to see it in full size.
![]() Fractals generated by iterated affine transformations
Fractals generated by iterated affine transformations
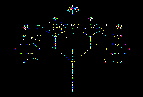 Program TreeX.bas The fractal tree
Program TreeX.bas The fractal tree
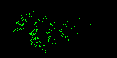 Program FernX.bas An example of fern
Program FernX.bas An example of fern
 Program MountainsX.bas A mountain
chain with snow at high quote
Program MountainsX.bas A mountain
chain with snow at high quote
 Another mountain chain example
Another mountain chain example
![]()
![]()
![]() You must click on each image if you want to see it in full size.
You must click on each image if you want to see it in full size.
You can continue by yourself to explore the wonderful universe of fractals on your personal computer. If you have a fast machine and a good screen resolution you will get better and better images! Some of them will be realistic, other will be only of mathematical interest, some other will be elegant and decorative...
While waiting that the Fractal Gallery become larger and recher of pictures you may build up your own.